Содержимое материала:

Классическое определение вероятности
Решение задач.
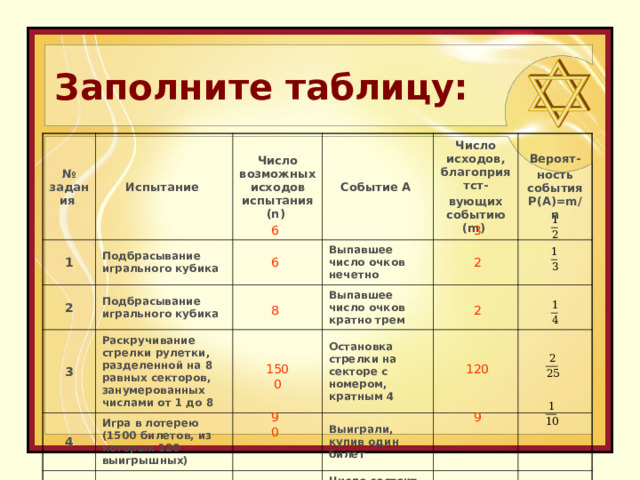
Заполните таблицу:
№ задания
Испытание
1
Подбрасывание игрального кубика
Число возможных исходов испытания ( n )
2
Событие А
Подбрасывание игрального кубика
3
Выпавшее число очков нечетно
Раскручивание стрелки рулетки, разделенной на 8 равных секторов, занумерованных числами от 1 до 8
4
Число исходов, благоприятст-
вующих событию ( m )
Игра в лотерею (1500 билетов, из которых 120 выигрышных)
5
Выпавшее число очков кратно трем
Вероят-
ность события Р(А)= m / n
Остановка стрелки на секторе с номером, кратным 4
Случайный выбор двузначного числа
Выиграли, купив один билет
Число состоит из одинаковых цифр
6
3
6
2
8
2
1500
120
90
9

Практикум по решению задач.
Задача 1.
Таня забыла последнюю цифру номера телефона знакомой девочки и набрала ее наугад. Какова вероятность того, что Таня попала к своей знакомой?
Решение.

Практикум по решению задач.
Задача 2.
На четырех карточках написаны буквы О, Т, К, Р. Карточки перевернули и перемешали. Затем открыли наугад последовательно эти карточки и положили в ряд. Какова вероятность того, что получится слово «КРОТ»?
Решение.
Исходы – все возможные перестановки из четырех элементов (О, Т, К, Р); общее число исходов:
Событие А = {после открытия карточек получится слово «КРОТ»}:
О
Т
К
Р

Практикум по решению задач.
Задача 3.
На четырех карточках написаны цифры 1, 2, 3, 4. Карточки перевернули и перемешали. Затем открыли наугад последовательно три карточки и положили в ряд. Какова вероятность того, что в результате получилось: а) число 123; б) число 312 или 321; в) число, первая цифра которого 2?
Решение.
Исходами опыта являются все возможные размещения четырех карточек на трех местах (порядок расположения важен). Общее число исходов:
1
2
3
4
б) Событие В={ из трех карточек образовано число 312 и 321},

Практикум по решению задач.
Задача 3.
На четырех карточках написаны цифры 1, 2, 3, 4. Карточки перевернули и перемешали. Затем открыли наугад последовательно три карточки и положили в ряд. Какова вероятность того, что в результате получилось: а) число 123; б) число 312 или 321; в) число, первая цифра которого 2?
Решение.
1
2
Рассмотрим события и их вероятности:
а) Событие А={из трех карточек образовано число 123},
3
4
б) Событие В={ из трех карточек образовано число 312 и 321},

Практикум по решению задач.
Задача 3.
На четырех карточках написаны цифры 1, 2, 3, 4. Карточки перевернули и перемешали. Затем открыли наугад последовательно три карточки и положили в ряд. Какова вероятность того, что в результате получилось: а) число 123; б) число 312 или 321; в) число, первая цифра которого 2?
Решение.
1
2
б) Событие В={ из трех карточек образовано число 312 и 321},
3
4
б) Событие В={ из трех карточек образовано число 312 и 321},

Практикум по решению задач.
Задача 3.
На четырех карточках написаны цифры 1, 2, 3, 4. Карточки перевернули и перемешали. Затем открыли наугад последовательно три карточки и положили в ряд. Какова вероятность того, что в результате получилось: а) число 123; б) число 312 или 321; в) число, первая цифра которого 2?
Решение.
1
2
в)Событие С={из трех карточек образовано число, первая цифра которого 2}. Если первая цифра фиксирована, то на оставшихся двух местах можно разместить любую из оставшихся трех цифр (с учетом порядка), то есть
3
4
б) Событие В={ из трех карточек образовано число 312 и 321},

Практикум по решению задач.
Задача 4.
В ящике лежат 1 белый и три черных шара. Наугад вынимаются 2 шара. Какова вероятность того, что вынуты: 1) 2 черных шара; 2) белый и черный шар?
Решение.
Исходы – все возможные пары шаров . Общее число исходов
1) Событие А={вынуты два черных шара};
2) Событие В={вынуты белый и черный шары};

Практикум по решению задач.
Задача 5.
C лучайным образом одновременно выбираются две буквы из 33 букв русского алфавита. Найдите вероятность того, что: 1) обе они согласные; 2) среди них есть «ъ»; 3) среди них нет «ъ»; 4) одна буква гласная, а другая согласная.
Решение.
1) А={ обе выбранные буквы – согласные}. В русском языке 21 согласная буква, 10 гласных и 2 буквы («ь», «ъ») не обозначающие звуков.

Практикум по решению задач.
Задача 5.
C лучайным образом одновременно выбираются две буквы из 33 букв русского алфавита. Найдите вероятность того, что: 1) обе они согласные; 2) среди них есть «ъ»; 3) среди них нет «ъ»; 4) одна буква гласная, а другая согласная.
Решение.
2) В={среди выбранных букв есть «ъ»}.

Практикум по решению задач.
Задача 5.
C лучайным образом одновременно выбираются две буквы из 33 букв русского алфавита. Найдите вероятность того, что: 1) обе они согласные; 2) среди них есть «ъ»; 3) среди них нет «ъ»; 4) одна буква гласная, а другая согласная.
Решение.
3) С={среди выбранных букв нет «ъ»}.

Практикум по решению задач.
Задача 5.
C лучайным образом одновременно выбираются две буквы из 33 букв русского алфавита. Найдите вероятность того, что: 1) обе они согласные; 2) среди них есть «ъ»; 3) среди них нет «ъ»; 4) одна буква гласная, а другая согласная.
Решение.
4) D ={среди выбранных букв одна буква гласная, а другая согласная}.

Дополнительные задачи:
Задача 1. Четыре билета на елку распределили по жребию между 15 мальчиками и 12 девочками. Какова векроятность того, что билеты достанутся 2 мальчикам и 2 девочкам?
Задача 2. Случайно нажимают три клавиши из одной октавы. Найдите вероятность того, что:
звучат ноты «си» и «до»;
не звучит нота «фа»;
звучит нота «ля»;
получится до-мажорное звучание.